Lũy thừa ~a^n~ (đọc là ~a~ mũ ~n~) là tích của ~n~ thừa số ~a~, nghĩa là ~a^n = a \times a\times...\times a~ (~n~ thừa số ~a~). Quy ước: ~a^0 = 1~.

Ví dụ: ~2^4 = 2×2×2×2=16~

Nam rất thích các bài toán về lũy thừa. Trong ngày kỷ niệm ~49~ năm giải phóng thành phố Đà Nẵng 29/3/1975 - 29/3/2024, Nam đố Mai bài toán như sau: Cho một số tự nhiên ~n~, tìm chữ số cuối của phép lũy thừa ~2903~ mũ ~n~.

Bạn là người giỏi lập trình, hãy giúp Mai giải bài toán này nhé!

Dữ liệu

• Nhập từ bàn phím số nguyên ~n~ ~(n < 10^{10})~.

Kết quả

• In ra màn hình chữ số cuối của giá trị ~2903^n~.

Sample Input 1

1

Sample Output 1

3

Note

Chữ số cuối của ~2903^1 = 2903~ là ~3~.

Sample Input 2

2

Sample Output 2

9

Note

Chữ số cuối của ~2903^2 = 8427409~ là ~9~.

Một xâu ~S_1~ là xâu con của một xâu ~S_2~ nếu ~S_1~ là một chuỗi các ký tự liên tiếp của ~S_2~.

Ví dụ: bc là xâu con của abcd.

Cho xâu ~S_1~ và ~S_2~. Hãy tìm vị trí xuất hiện cuối cùng của xâu con ~S_1~ trong ~S_2~.

Dữ liệu

• Dòng thứ nhất ghi xâu ~S_1~,
• Dòng thứ hai ghi xâu ~S_2~.

Kết quả

• Nếu ~S_1~ là xâu con của xâu ~S_2~ thì in ra vị trí xuất hiện cuối cùng của ~S_1~ trong ~S_2~. Nếu không phải thì in ra 0.

Sample Input

abc
abcabcbc

Sample Output

4

Note

~S_1 =~ abc; ~S_2 =~ abcabcbc. Vị trí xuất hiện cuối cùng của xâu ~S_1~ trong xâu ~S_2~ là vị trí thứ ~4~: abcabcbc

Cho bảng hình vuông kích thước ~N×N~. Người ta điền ~N×N~ số đầu tiên của dãy ~1~, ~3~, ~5~, ~...~ vào bảng theo hình xoắn ốc từ ngoài vào trong, theo chiều kim đồng hồ bắt đầu từ ô góc trái bên trên. Hình bên dưới là minh họa cho bảng kích thước ~4×4~ và ~5×5~ tương ứng.

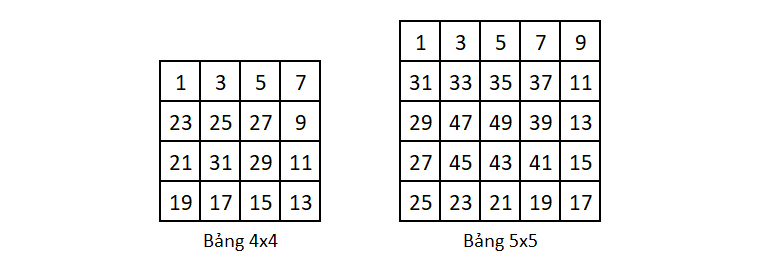
Hãy tính tổng các số lớn nhất trên mỗi dòng của bảng.

Dữ liệu

• Nhập từ bàn phím một số nguyên dương ~N~ ~(1 ≤ N ≤10000)~.

Kết quả

• In ra màn hình một số nguyên dương là tổng các số lớn nhất trên mỗi dòng của bảng.

Sample Input 1

4

Sample Output 1

84

Note

• Với ~N = 4~, các số lớn nhất trên mỗi dòng của bảng lần lượt là ~7~, ~27~, ~31~, ~19~ có tổng là ~84~.

Sample Input 2

5

Sample Output 2

165

Note

• Với ~N = 5~, các số lớn nhất trên mỗi dòng của bảng lần lượt là ~9~, ~37~, ~49~, ~45~, ~25~ có tổng là ~165~.