Bác Tư là một người thợ lát gạch nổi tiếng. Một hôm, bác nhận được đơn đặt hàng đặc biệt từ trường học trong làng: lát một sân chơi hình vuông thật đẹp để các em học sinh có chỗ vui chơi.

Bác Tư này ra một ý tưởng độc đáo: lát gạch thành từng lớp hình vuông đồng tâm - lớp ngoài to, rồi lớp nhỏ dần vào giữa, và cứ cách một lớp thì đổi màu. Để tạo điểm nhấn, bác quyết định bắt đầu từ lớp ngoài cùng là gạch màu xanh, rồi xen kẽ với gạch trắng, cứ thể vào đến lớp trung tâm. Sân chơi được chia thành những ô vuông nhỏ bằng nhau, tạo thành một hình vuông lớn có kích thước ~N \times N~, trong đó ~N~ là số lẻ để có thể lát đến đúng ô trung tâm.

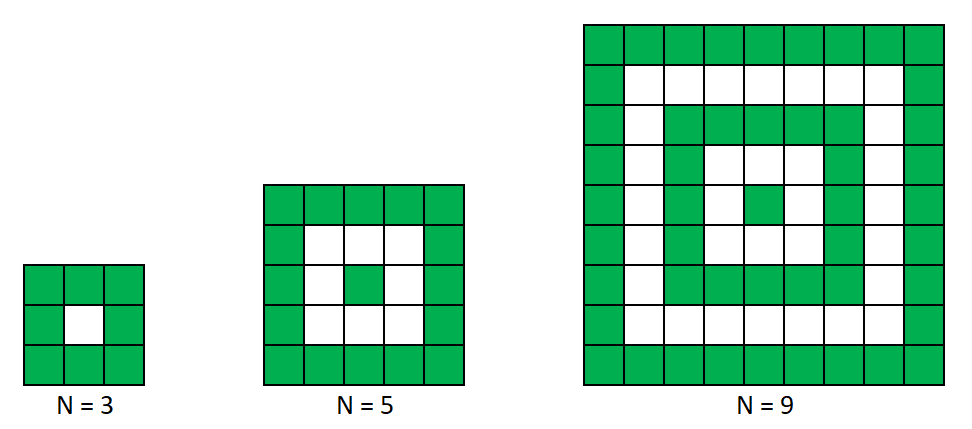
Yêu cầu: Biết rằng bác Tư đã lát gạch theo đúng ý tưởng như trên (như hình vẽ), em hãy giúp bác:

• Tính số ô được lát bằng gạch màu.
• Tính số ô còn lại là gạch trắng.

Input

• Một số nguyên lẻ ~N~ ~(3 ≤ N ≤ 10^8)~.

Output

• Một dòng gồm hai số là số ô gạch trắng và số ô gạch màu.

Sample Input 1

3

Sample Output 1

1 8

Note

• Với ~N = 3~ số ô gạch trắng là ~1~, số ô gạch màu là ~8~.

Sample Input 2

9

Sample Output 2

32 49

Note

• Với ~N = 9~ số ô gạch trắng là ~32~, số ô gạch màu là ~49~.

Nhân dịp kỷ niệm 50 năm Ngày Giải phóng miền Nam, thống nhất đất nước (30/4/1975 - 30/4/2025), trường em tổ chức buổi giao lưu học sinh các khối. Mỗi học sinh được đánh số từ ~1~ đến ~N~.

Yêu cầu: Trong buổi giao lưu các bạn học sinh bắt tay đoàn kết mừng lễ 30/4, cụ thể như sau:

• Học sinh có số chẵn chỉ được bắt tay với học sinh số lẻ (và ngược lại).
• Mỗi học sinh chỉ được bắt tay tối đa ~K~ lần.
• Mỗi cặp học sinh chỉ bắt tay nhau ~1~ lần duy nhất.

Hãy tính tổng số cái bắt tay có thể diễn ra trong buổi giao lưu.

Input

• Hai dòng, mỗi dòng chứa một số nguyên lần lượt là ~N~ - tổng số học sinh ~(2 ≤ N ≤ 100)~ và ~K~ - số lần bắt tay tối đa của mỗi học sinh ~(1 ≤ K ≤ N)~.

Output

• Một số nguyên là tổng số cái bắt tay diễn ra.

Sample Input 1

5
5

Sample Output 1

6

Note

• Có ~2~ học sinh chẵn: ~2~, ~4~, có ~3~ học sinh lẻ: ~1~, ~3~, ~5~, tổng cặp chẵn lẻ: ~6~ → tất cả đều được vì không vượt quá ~K = 5~.

Sample Input 1

6
3

Sample Output 1

9

Note

• Có ~3~ học sinh chẵn: ~2~, ~4~, ~6~ và ~3~ học sinh lẻ: ~1~, ~3~, ~5~. Mỗi học sinh được bắt tay ~3~ lần → tối đa tất cả các cặp chẵn lẻ đều được.

Các số nguyên dương được xếp vào ma trận vô hạn theo quy luật như hình minh họa dưới đây.

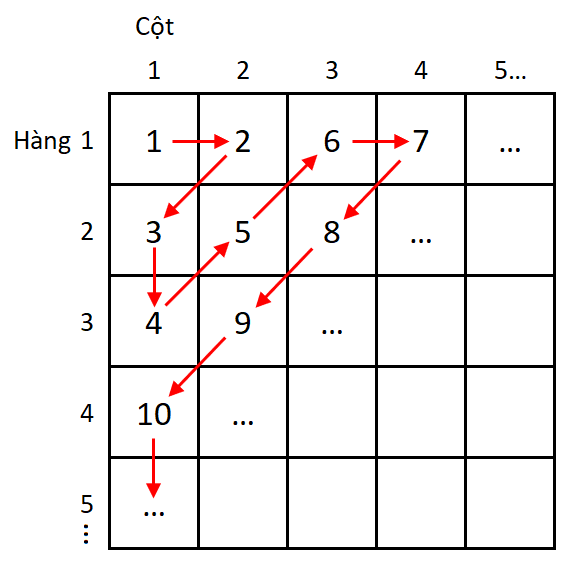
Ví dụ:

• Số ~1~ ở hàng ~1~, cột ~1~.
• Số ~2~ ở hàng ~1~, cột ~2~.
• Số ~3~ ở hàng ~2~, cột ~1~.
• Số ~4~ ở hàng ~3~, cột ~1~.
• Số ~5~ ở hàng ~2~, cột ~2~.
• Số ~6~ ở hàng ~1~, cột ~3~.
• ~...~

Yêu cầu: Viết chương trình nhập vào một số nguyên dương ~N~ ~(1 ≤ N ≤ 10^6)~. Hãy xác định, hãy xác định vị trí của số ~N~ trong bảng: hàng mấy, cột mấy?

Input

• Một số nguyên dương ~N~ ~(1 ≤ N ≤ 10^6)~.

Output

• Một dòng chứa hai số nguyên lần lượt là hàng và cột chứa số ~N~.

Sample

Input 1

25

Output 1

4 4

Input 2

100

Output 2

9 6

Trong một trò chơi rèn luyện tư duy số học có tên là chữ số cuối cùng, người chơi bắt đầu với một số tự nhiên ~X~. Họ sẽ liên tục thay thế ~X~ bằng tổng các chữ số của nó cho đến khi kết quả cuối cùng là một số có một chữ số duy nhất.

Ví dụ: số ~X = 395~ sẽ thay được bởi số ~X=3+9+5=17~, sau đó lại thay số ~X = 17~ bởi ~X=1+7=8~ thì kết thúc.

Yêu cầu: Trong phần tiếp theo của trò chơi, người chơi nhận được một số tự nhiên ~N~. Đếm có bao nhiêu cách cắt số ~N~ thành hai phần liên tiếp: phần đầu và phần cuối (không để trống phần nào) sao cho chữ số cuối cùng của phần cuối lớn hơn phần đầu.

Input

• Một dòng ghi số tự nhiên ~N~ ~(10 ≤ N ≤ 10^9)~.

Output

• Số cách cắt ~N~ thỏa mãn yêu cầu đề bài. Nếu không có cách nào thỏa mãn, in số 0.

Sample Input 1

234

Sample Output 1

1

Note

• Có thể cắt số ~234~ thành:
  • ~2~ và ~34~: có chữ số cuối cùng ~2 < 7~ (thỏa mãn)
  • ~23~ và ~4~: có chữ số cuối cùng ~5 > 4~ (không thỏa mãn)

Sample Input 2

33

Sample Output 2

0

Note

• Chỉ có thể cắt số ~33~ thành ~3~ và ~3~: có chữ số cuối cùng ~3 = 3~ (không thỏa mãn).