Đường chéo
Xem dạng PDF
Gửi bài giải
Điểm:
1,00 (OI)
Giới hạn thời gian:
1.0s
Giới hạn bộ nhớ:
512M
Input:
stdin
Output:
stdout
Dạng bài
Ngôn ngữ cho phép
Python, Scratch
Cho bảng kích thước ~N × N~. Mỗi ô được đánh một số tự nhiên từ ~1~ đến ~N × N~ theo quy luật như hình dưới đây. Mỗi ô sẽ thuộc vào duy nhất một đường chéo (từ trái dưới đến phải trên).
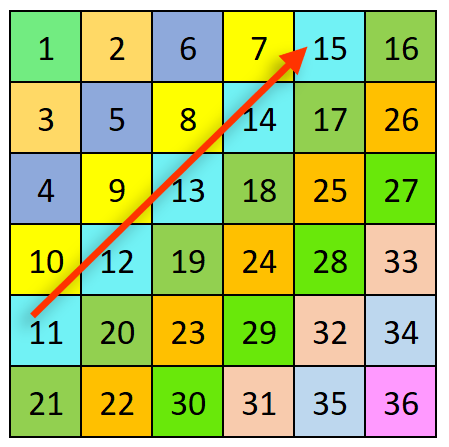
Cho số ~K~, hãy tính tổng các số có trong đường chéo chứa số ~K~.
Dữ liệu
- Gồm hai số tự nhiên ~N~ và ~K~ ~(1 ≤ N ≤ 10^5; K ≤ N × N)~, mỗi số trên một dòng.
Kết quả
- Gồm một số tự nhiên là kết quả của bài toán.
Chấm điểm
- Có 30% số test ứng với 30% số điểm: ~N ≤ 10~;
- 30% số test khác ứng với 30% số điểm: ~N ≤ 100~;
- 40% số test còn lại ứng với 40% số điểm không có ràng buộc gì thêm.
Sample
Input 1
6
8
Output 1
34
Note
- ~7+8+9+10 = 34~
Input 2
6
34
Output 2
69
Note
- ~34+35=69~
Bình luận
mày tên gì
gửi cho đoàn hoàng coi
code bình dương à
Code nè:
def findposition(N, K): count = 0 for s in range(2, 2 * N + 1): if s <= N + 1: num = s - 1 else: num = 2 * N - s + 1 if count + num >= K: posindiag = K - count if s <= N + 1: i = s - posindiag j = posindiag else: i = N - posin_diag + 1 j = s - i return i, j count += num return -1, -1
def diagonalsum(N, K): i, j = findposition(N, K) s = i + j if s <= N + 1: num = s - 1 else: num = 2 * N - s + 1 count = 0 for t in range(2, s): if t <= N + 1: count += t - 1 else: count += 2 * N - t + 1 start = count + 1 end = start + num - 1 return (start + end) * num // 2
N = int(input()) K = int(input()) print(diagonal_sum(N, K))